## 840. 矩阵中的幻方
### 题目描述
`3 x 3` 的幻方是一个填充有 从 1 到 9 的不同数字的 `3 x 3` 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。
给定一个由整数组成的row x col 的 grid,其中有多少个 `3 × 3` 的 “幻方” 子矩阵?
注意:虽然幻方只能包含 1 到 9 的数字,但 grid 可以包含最多15的数字。
### 示例
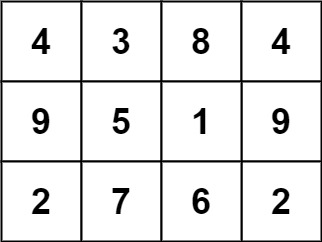
输入: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]]
输出: 1
解释:
下面的子矩阵是一个 3 x 3 的幻方:
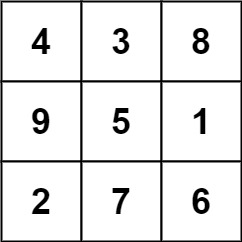
示例 2:
输入: grid = [[8]]
输出: 0
提示:
row == grid.length
col == grid[i].length
1 <= row, col <= 10
0 <= grid[i][j] <= 15
### 解题思路
以`3x3`网格的窗口滑动,以网格的中心往外扩散,满足题目要求的条件有:
- 中心值必须为5;
- `3x3`网格中的所有元素必须在1~9内;
- `3x3`网格的行、列、对角线的和必须为15;
### 代码
```C++
#include <vector>
#include <iostream>
using namespace std;
class Solution {
public:
int numMagicSquaresInside(vector<vector<int>>& grid) {
int rows = grid.size();
int cols = grid[0].size();
int count = 0;
for (int r = 0; r < rows - 2; r++) {
for (int c = 0; c < cols - 2; c++) {
if (grid[r + 1][c + 1] != 5) {
continue;
}
if (isMagicSquare(
grid[r][c], grid[r][c + 1], grid[r][c + 2],
grid[r + 1][c], grid[r + 1][c + 1], grid[r + 1][c + 2],
grid[r + 2][c], grid[r + 2][c + 1], grid[r + 2][c + 2]
)) {
count++;
}
}
}
return count;
}
private:
bool isMagicSquare(int a, int b, int c, int d, int e, int f, int g, int h, int i) {
vector<int> vals = {a, b, c, d, e, f, g, h, i};
vector<int> frequency(16, 0);
for (int value : vals) {
if (value < 1 || value > 9) {
return false;
}
frequency[value]++;
}
for (int num = 1; num <= 9; num++) {
if (frequency[num] != 1) {
return false;
}
}
return (a + b + c == 15 && // 第一行
d + e + f == 15 && // 第二行
g + h + i == 15 && // 第三行
a + d + g == 15 && // 第一列
b + e + h == 15 && // 第二列
c + f + i == 15 && // 第三列
a + e + i == 15 && // 主对角线
c + e + g == 15); // 副对角线
}
};
int main(){
Solution solution;
std::vector<int> row1 = {4,3,8,4};
std::vector<int> row2 = {9,5,1,9};
std::vector<int> row3 = {2,7,6,2};
std::vector<std::vector<int>> in = {row1, row2, row3};
int ans = solution.numMagicSquaresInside(in);
std::cout << "answer is: " << ans << endl;
}
```

840. 矩阵中的幻方

