在计算机科学里,树的遍历(也称为树的搜索)是图的遍历的一种,指的是按照某种规则,不重复地访问某种树的所有节点的过程。具体的访问操作可能是检查节点的值、更新节点的值等。不同的遍历方式,其访问节点的顺序是不一样的。
与那些基本上都有标准遍历方式(通常是按线性顺序)的线性数据结构(如链表、一维数组)所不同的是,树结构有多种不同的遍历方式。从二叉树的根节点出发,节点的遍历分为三个主要步骤:对当前节点进行操作(称为“访问”节点)、遍历左边子节点、遍历右边子节点。这三个步骤的先后顺序也是不同遍历方式的根本区别。
遍历方式的命名,源于其访问节点的顺序。最简单的划分是:**深度优先DFS**(先访问子节点,再访问父节点,最后是第二个子节点)和**广度优先BFS**(先访问第一个子节点,再访问第二个子节点,最后访问父节点)。深度优先可进一步按照根节点相对于左右子节点的访问先后来划分。如果把左节点和右节点的位置固定不动,那么根节点放在左节点的左边,称为**前序**(pre-order)、根节点放在左节点和右节点的中间,称为**中序**(in-order)、根节点放在右节点的右边,称为**后序**(post-order)。对广度优先而言,遍历没有前序中序后序之分:给定一组已排序的子节点,其“广度优先”的遍历只有一种唯一的结果,广度优先遍历也称为**层序遍历**。本文中用到的树结构如下图
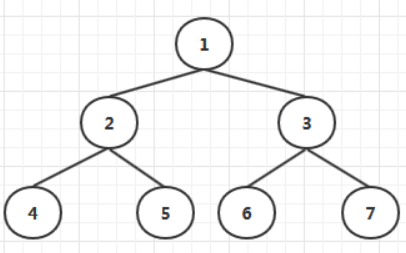
**树结构的定义:**
```java
package online.miantiao;
/**
* @author miantiao
* @time 2020年7月3日 下午11:46:38
*/
public class TreeNode<T> {
public T val;
public TreeNode left;
public TreeNode right;
public TreeNode(T val) {
this.val = val;
}
}
```
**树的创建:**
```java
package online.miantiao;
/**
* @author miantiao
* @time 2020年7月3日 下午11:50:07
*/
public class TraverseTree {
public TreeNode<Integer> createTree() {
TreeNode<Integer> root = new TreeNode<Integer>(1);
TreeNode<Integer> node2 = new TreeNode<Integer>(2);
TreeNode<Integer> node3 = new TreeNode<Integer>(3);
root.left = node2;
root.right = node3;
TreeNode<Integer> node4 = new TreeNode<Integer>(4);
TreeNode<Integer> node5 = new TreeNode<Integer>(5);
node2.left = node4;
node2.right = node5;
TreeNode<Integer> node6 = new TreeNode<Integer>(6);
TreeNode<Integer> node7 = new TreeNode<Integer>(7);
node3.left = node6;
node3.right = node7;
return root;
}
}
```
### 一、深度优先遍历
深度优先遍历顾名思义,指的是从根节点出发,沿着左子树方向进行纵向遍历,直到找到叶子节点为止。然后回溯到前一个节点,进行右子树节点的遍历,直到遍历完所有可达节点为止。根据节点访问顺序,深度优先遍历可以划分为:
- 先序遍历;
- 中序遍历;
- 后序遍历。
#### 1、先序遍历
先序遍历指先访问根节点,然后访问左子树,再访问右子树的遍历方式。下图所示的树结构,先序遍历的结果为:1,2,4,5,3,6,7。
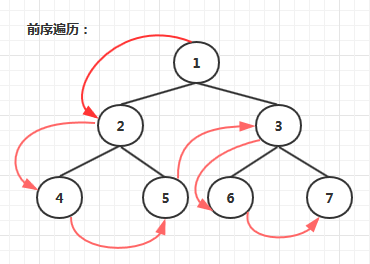
**代码实现(递归):**
```java
/**
* 树的先序遍历
*/
public void PreOrder(TreeNode<Integer> root){
if (root == null){
return;
}
System.out.println(root.val);
PreOrderRecur(root.left);
PreOrderRecur(root.right);
}
```
#### 2、中序遍历
中序遍历指先访问左子树,然后访问根节点,再访问右子树的遍历方式。下图所示的树结构,先序遍历的结果为:4,2,5,1,6,3,7。
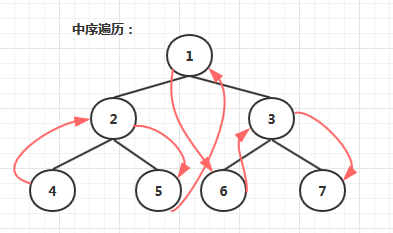
**代码实现(递归):**
```java
/**
* 树的中序遍历
*/
public void InOrder(TreeNode<Integer> root){
if (root == null){
return;
}
InOrder(root.left);
System.out.println(root.val);
InOrder(root.right);
}
```
#### 3、后序遍历
后序遍历指先访问左子树,然后访问右子树,再访问根节点的遍历方式。下图所示的树结构,先序遍历的结果为:4,5,2,6,7,3,1。

**代码实现(递归):**
```java
/**
* 树的后序遍历
*/
public void PostOrder(TreeNode<Integer> root){
if (root == null){
return;
}
InOrder(root.left);
InOrder(root.right);
System.out.println(root.val);
}
```
### 二、广度优先遍历
和深度优先遍历不同,广度优先遍历会先访问离根节点最近的节点。二叉树的广度优先遍历直观上是一层一层往下遍历,所以又称层次遍历。算法需借助队列实现。下图所示的树结构,广度优先遍历的结果为:1,2,3,4,5,6,7。

**代码实现(递归):**
```java
/**
* 树的广度优先遍历
*/
public void levelOrder(TreeNode<Integer> root) {
Queue<TreeNode<Integer>> queue = new ArrayDeque<TreeNode<Integer>>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode<Integer> node = queue.poll();
System.out.println(node.val);
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
```

树的遍历算法


